Breadth-First Traversal with Alternating Directions at Each Level

Yesterday I discussed the interview coding problem I blew: Code, in Java, a breadth-first traversal of a binary tree, alternating directions at each level.

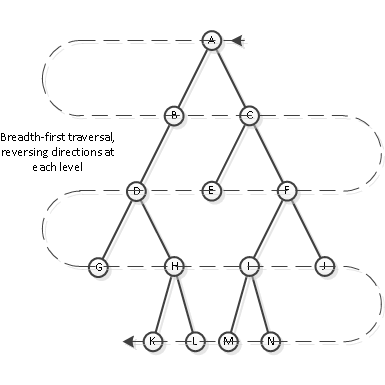
The key observation is obvious: At each level you process nodes in the reverse order of the previous level.  (Duh! That’s the problem statement.)  To turn it around: At each level you must preserve for later processing the child nodes in reverse order of the nodes you’re processing at this level.  A data structure which let’s you pull off nodes in reverse order in which you saved them is a stack, one of the simplest data structures of all.

In this case, we’re going to have at any given time two stacks: one we’re pulling nodes off of, and one we’re pushing nodes on to.  We know we’re at the end of a level when the stack we’re pulling nodes off of is empty, at that time we swap stacks and start pulling off the other one and pushing to the first one.  Each stack is used alternately, therefore is always processing nodes in the same direction.  We have a L→R stack and a R→L stack.  We’re done when we swap stacks and the new pull-from stack is empty.

If we were going to do this in a procedural fashion we’d have a function that held two stacks, and popped and pushed, and swapped.  But it is easy to do it in an O-O fashion, and if we do, we notice that the code for the two stacks is identical except for the order in which the child nodes are pushed onto the other stack—that’s the point of the observation that each stack is always used in the same direction.

So we’ve got two stacks identical except for the order in which they push the child nodes: that tells us we’re going to use an abstract class with two concrete subclasses, one for each direction.  And each stack pulls nodes off of itself and pushes them onto the other: So each stack holds a reference to the other.  In short, we’re going to have something that looks like this—note we directly extend an existing collection class that implements Stack<>:

abstract class Level extends ArrayDeque<Node<D>> {
   public Level other;

   public Level doLevel() {
      ...
   }
}

final Level lr = new Level() { ... };
final Level rl = new Level() { ... };

lr.other = rl;
rl.other = lr;

Now, assume we have a standard node with children left and right, then we want to arrange that the two subclasses process the children in the opposite order.  We do it like this (it would be easier in a language with pointer-to-methods):

abstract class Level extends ArrayDeque<Node<D>> {
   ...
   protected abstract Node<D> first(Node<D> n);
   protected abstract Node<D> second(Node<D> n);
   ...
}

final Level lr = new Level() {
   protected Node<D> first(Node<D> n) { return n.left; }
   protected Node<D> second(Node<D> n) { return n.right; }
}

final Level rl = new Level() { 
   protected Node<D> first(Node<D> n) { return n.right; }
   protected Node<D> second(Node<D> n) { return n.left; }
}

And the processing method will use first() and second() rather than left and right.  Processing is really easy: we pull a node off the queue, and then visit and push each child:

public void doNode(Node<D> n) {
   if (null != n) {
      visit.it(n.data);
      other.push(n);
   }
}

public Level doLevel() {
   while (!isEmpty()) {
      final Node<D> n = pop();
      doNode(first(n));
      doNode(second(n));
   }
   clear();
   return other;
}

Of course this goes in the abstract class Level, not the subclasses that specify the direction.

Note that doLevel() returns the other stack when it is done processing all the nodes on itself.  This makes the main loop rather simple:

rl.doNode(root);
Level stk = lr;
while (!stk.isEmpty()) {
   stk = stk.doLevel();
}

After initializing one of the stacks with the root node, this code starts with the other and then bounces from one to the other until it finds no more nodes to process.  That’s it!  Full code is here.

I would point out that the standard Java library’s ArrayDeque<> is nowhere near as nice an implementation as the standard C++ std::deque class.  The C++ variant doesn’t store the entire queue in a single contiguous array: instead it uses chunks of elements (“decks”) that are chained together.  This means that the queue can not only grow as needed, it can shrink as needed too.  In contrast, ArrayDeque<> can only grow, and not only that, the clear() method doesn’t shrink it!  In fact there’s no way to shrink its array of elements.

Thus, if you use ArrayDeque<> as the base Stack<> for this code the two stacks will grow to the size of the widest level they process.  If the tree you’re processing is very “bushy” that could be quite a lot of memory in use at one time, maybe twice what is necessary (even three times what is necessary for the instant that one of the stacks needs to grow its array).  Consider finding a different Stack that can grow and shrink.  For example, you might adapt my queue that you can find in this post.